Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
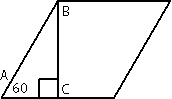Рассмотрим треугольник АВС.
Этот треугольник
прямоугольный (по условию задачи).
∠A=60°, следовательно по
теореме о сумме углов треугольника:
∠АВС = 180°-90°-60°=30°.
По второму свойству прямоугольного треугольника:
АС=АВ/2=32/2=16.
Следовательно вторая половина стороны ромба = 32-16=16.
Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: 16 и 16.
Поделитесь решением
Присоединяйтесь к нам...
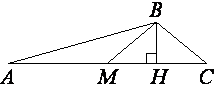В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
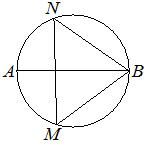На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
Найдите площадь треугольника, изображённого на рисунке.
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: