В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=35°+58°=93°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, ∠BAD=∠ADC=93°.
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ABD+∠BDA
180°=93°+∠ABD+35°
∠ABD=180°-93°-35°
∠ABD=52°
Ответ: 52
Поделитесь решением
Присоединяйтесь к нам...
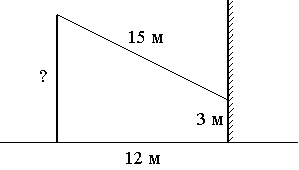От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
В треугольнике ABC угол C равен 90°, BC=5, AC=2.
Найдите tgB.
Найдите площадь треугольника, изображённого на рисунке.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Косинус острого угла A треугольника ABC равен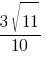 
. Найдите sinA.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: