В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
По второму свойству четырехугольника:
AB+CD=BC+AD=16
По
определению средней линии трапеции: m=(BC+AD)/2=16/2=8
Ответ: m=8
Поделитесь решением
Присоединяйтесь к нам...
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
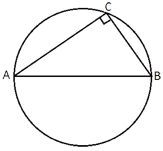В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
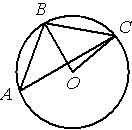Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
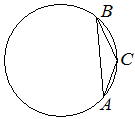В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: