В трапеции ABCD AB=CD, ∠BDA=67° и ∠BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=67°+28°=95°
Т.к. AB=CD, то
трапеция ABCD -
равнобедренная.
Тогда ∠ADC=∠BAD=95° (по
свойству равнобедренной трапеции).
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ADB+∠ABD
180°=95°+67°+∠ABD
∠ABD=18°
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
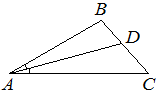В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC угол C прямой, AC=4, cosA=0,8. Найдите AB.
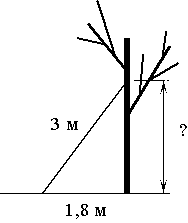Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
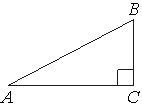В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: