
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
/NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 64°*2=128°.
Тогда дуга NB равна 180°-128°=52°
/NMB - тоже
вписанный в окружность, следовательно он равен 52°/2=26°
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
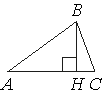 В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
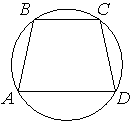 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Комментарии: