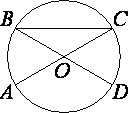
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
∠AOB -
смежный углу AOD. Следовательно:
∠AOB=180°-∠AOD=180°-132°=48°
∠AOB является
центральным, и следовательно равен градусной мере дуги, на которую опирается.
∠ACB -
вписанный угол, и следовательно равен половине градусной меры дуги, на которую он опирается.
∠ACB=48°/2=24°
Ответ: 24
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
Сторона ромба равна 20, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Стороны AC, AB, BC треугольника ABC равны 2√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: