
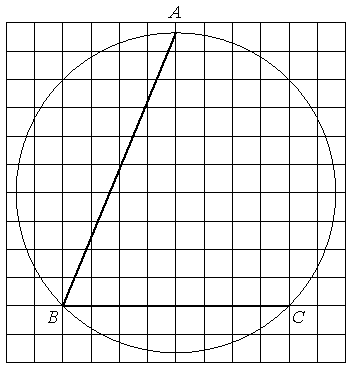
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
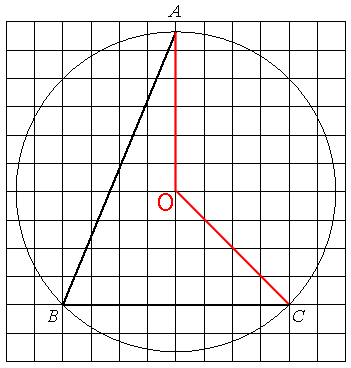 Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC равен 135° (прямой угол + половина от прямого угла, 90°+45°=135°).
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается, тоже равна 135°.
∠ABC -
вписанный угол и по
теореме равен 135°/2=67,5°
Ответ: 67,5
Поделитесь решением
Присоединяйтесь к нам...
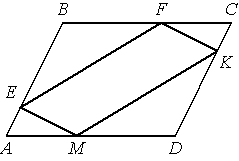 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=84 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=84 и BC=BM. Найдите AH.
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
 естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
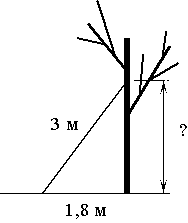 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?

Комментарии: