Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
Пусть:
∠KMP=62°
∠MKP=54°
∠KPM=64°
Рассмотрим треугольник AMK.
AM=AK (по
второму свойству касательной)
Следовательно треугольник AMK -
равнобедренный, тогда, по
свойству равнобедренного треугольника:
∠AMK=∠AKM
Заметим, что оба этих угла охватывают дугу MK, и следовательно равны половине ее градусной меры (по
свойству углов на окружности).
∠KPM является
вписанным в окружность углом и опирается на эту же дугу, следовательно и он равен половине градусной меры этой дуги.
Получается, что:
∠AMK=∠AKM=∠KPM=64°
Применив
теорему о сумме углов треугольника:
180°=∠AMK+∠AKM+∠MAK
180°=64°+64°+∠MAK
∠MAK=52°
Аналогично, для двух других треугольников получим:
∠BKP=∠BPK=∠KMP=62°
∠KBP=180°-62°-62°=56°
И...
∠CPM=∠CMP=∠MKP=54°
∠PCM=180°-54°-54°=72°
Ответ: 52°, 56° и 72°
Поделитесь решением
Присоединяйтесь к нам...
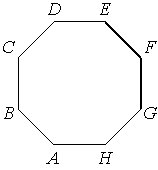ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
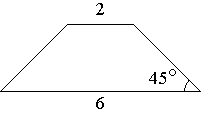В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
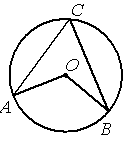Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: