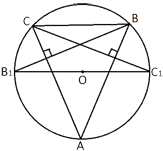
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
∠BAC является
вписанным углом и опирается на малую дугу CB.
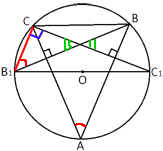
Проведем отрезок CB1, ∠CB1B тоже является
вписанным и опирается на ту же дугу, следовательно, ∠BAC=∠CB1B.
B1C1 является диаметром окружности, так как проходит через ее центр. Следовательно, B1C1 делит окружность на две дуги по 180°
∠B1CC1 тоже
вписанный и опирается на дугу в 180°, по
теореме о вписанном угле ∠B1CC1=180°/2=90°.
Обозначим еще три точки, как показано на рисунке ниже:
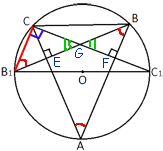Точки E и F - точки пересечения
высот и сторон треугольника ABC, G - точка пересечения
высот.
Рассмотрим треугольники B1CG и BFG.
∠CGB1=∠BGF (так как они
вертикальные).
∠B1CG=∠BFG (так как они оба прямые).
Следовательно, по
теореме о сумме углов треугольника, ∠СB1G=∠GBF
Следовательно, ∠GBF так же равен и ∠BAC
Рассмотрим треугольник AEB.
∠AEB=90° (так как BE -
высота).
∠BAC=∠GBF
Тогда, используя
теорему о сумме углов треугольника получаем, что каждый из углов BAC и GBF равен по 45°.
Ответ: ∠BAC=45°
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
Найдите площадь параллелограмма, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: