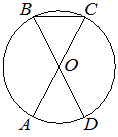
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
∠AOB -
смежный углу AOD. Следовательно:
∠AOB=180°-∠AOD=180°-50°=130°
∠AOB является
центральным, и следовательно равен градусной мере дуги, на которую опирается.
∠ACB -
вписанный угол, и следовательно равен половине градусной меры дуги, на которую он опирается.
∠ACB=130°/2=65°
Ответ: 65
Поделитесь решением
Присоединяйтесь к нам...
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
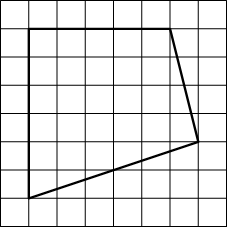Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: