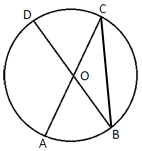В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
∠AOB -
смежный углу AOD. Следовательно:
∠AOB=180°-∠AOD=180°-128°=52°
∠AOB является
центральным, и следовательно равен градусной мере дуги, на которую опирается.
∠ACB -
вписанный угол, и следовательно равен половине градусной меры дуги, на которую он опирается.
∠ACB=52°/2=26°
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 2√
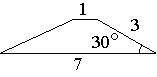Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 1 и 7.
В трапеции ABCD основания AD и BC равны соответственно 34 и 9, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=10.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
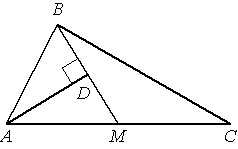Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: