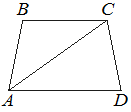
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
По
свойству равнобедренной трапеции, углы при основании равны.
Т.е. ∠B=∠C - это и есть наибольшие углы.
∠A=∠BAC+∠DAC=1°+46°=47°
AD||BC (по определению трапеции), следовательно боковую сторону AB можно рассматривать как секущую.
Тогда:
∠A+∠B=180° (так как это
внутренние углы).
∠B=180°-∠A=180°-47°=133°
Ответ: 133
Поделитесь решением
Присоединяйтесь к нам...
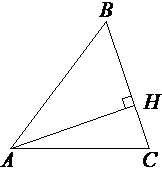В остроугольном треугольнике ABC высота AH равна 20√
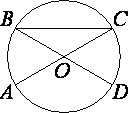В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
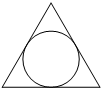Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
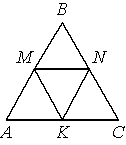В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: