Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
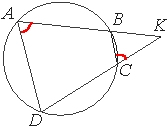По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по
свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB - является
смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.
Рассмотрим треугольникик AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
Тогда:
BK/DK=BC/AD
AD=(DK*BC)/BK=(12*6)/8=(3*6)/2=3*3=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
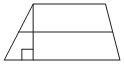Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
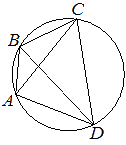Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: