Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
Рассмотрим треугольники ABC и KBM.
∠B - общий.
∠BAC=∠BKM (т.к. это
соответственные углы)
∠BCA=∠BMK (т.к. это тоже
соответственные углы)
Следовательно, эти треугольники
подобны по
первому признаку подобия.
Тогда по
определению подобных треугольников:
BA/BK=AC/KM
(BK+KA)/BK=AC/KM
1+KA/BK=AC/KM
1+2/1=AC/23
3=AC/23
AC=3*23=69
Ответ: AC=69
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь ромба, если его диагонали равны 39 и 2.
В треугольнике ABC угол C равен 90°, BC=5, AC=3.
Найдите tgB.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
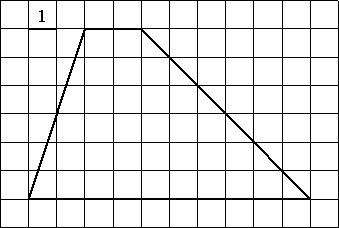Найдите площадь трапеции, изображённой на рисунке.
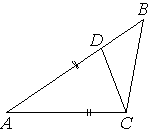Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: