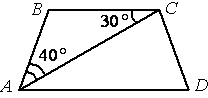Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
AD||BC (по
определению трапеции). Тогда AC является секущей для этих параллельных отрезков.
/BCA=/CAD, т.к. они
внутренние накрест-лежащие.
Тогда /BAD=30°+40°=70°.
По
свойству
равнобедренной трапеции /BAD=/ADC=70°.
Ответ: /ADC=70°.
Поделитесь решением
Присоединяйтесь к нам...
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
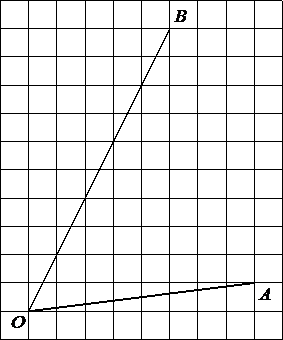Найдите тангенс угла
AOB.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
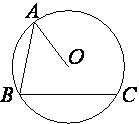Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: