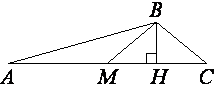В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
Так как BM -
медиана, значит AM=MC=AC/2=64/2=32
Рассмотрим треугольник MBC.
MH=MC-HC=32-16=16, т.е. получается, что MC=HC.
BH для этого треугольника получается не только
высота, но и
медиана. Это
свойство
равнобедренного треугольника.
По
свойству равнобедренного
треугольника: ∠BMC=∠ACB=37°.
∠AMB=180°-∠BMC=180°-37°=143° (т.к. он
смежный)
Ответ: 143
Поделитесь решением
Присоединяйтесь к нам...
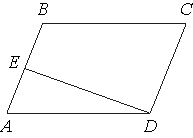Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
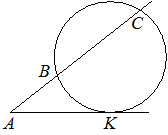Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
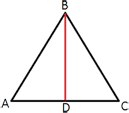Сторона равностороннего треугольника равна 10√
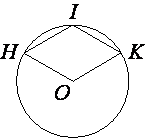Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: