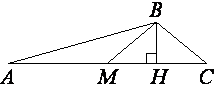В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
Так как BM -
медиана, значит AM=MC=AC/2=216/2=108
Рассмотрим треугольник MBC.
MH=MC-HC=108-54=54, т.е. получается, что MH=HC.
BH для этого треугольника получается не только
высота, но и
медиана. Это
свойство
равнобедренного треугольника.
По
свойству равнобедренного треугольника: ∠BMC=∠ACB=40°.
∠AMB=180°-∠BMC=180°-40°=140° (т.к. он
смежный)
Ответ: ∠AMB=140°
Поделитесь решением
Присоединяйтесь к нам...
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
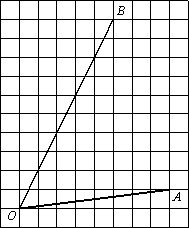Найдите тангенс угла AOB.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
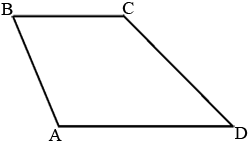Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-15 16:12:02) Администратор: Ольга.olg1851@yandex.ru, напишите, пожалуйста номер задачи (на fipi.ru) и страницу, что бы эту задачу можно было найти.
(2015-04-15 12:38:00) Администратор: Ольга.olg1851@yandex.ru, напишите, пожалуйста номер задачи (на fipi.ru) и страницу, что бы эту задачу можно было найти.
(2015-04-15 12:36:11) Администратор: Ольга, спасибо за найденную опечатку, исправлено.
(2015-04-15 10:59:55) Ольга.olg1851@yandex.ru: задачу решите пожалуйста. На стороне АВ треугольника АВС взята точка D так, что окружность, проходящая через точки А,С и D, касается прямой ВС. Найти АD, если АС=15, ВС=18 и СD= 10. Поиск по славам ничего не дал, хотя задача ФИПИ математика ОГЭ 2015. Спасибо
(2015-04-15 10:52:50) Ольга: исправьте ошибку в решении 374 МС = НС? МН=НС