Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
Рассмотрим каждое утверждение.
1) "Любой
параллелограмм можно вписать в окружность", это утверждение неверно, т.к. должно выполняться
условие об углах параллелограмма.
2) "Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны", это утверждение верно по
свойству углов.
3) "Точка пересечения двух окружностей равноудалена от центров этих окружностей", это утверждение неверно. По
определению окружности, все точки окружности равноудалены от центра, а точки пересечения окружностей, естественно, принадлежат окружностям, т.е. находятся от центров на расстоянии равном радиусам окружностей. Если окружности имеют разные радиусы, то точка пересечения находится на разных растояниях от центров.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
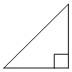В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл) | Прочее оборудование и монтаж | Средн. расход газа/ средн. потребл. мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 24 000 руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 000 руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт*ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости устройства газового и электрического отопления?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-03-09 16:33:57) Администратор: Татьяна, думаю, Вы правы. Я неверно истолковал утверждение. Исправлено. Спасибо большое, что поправили!!!
(2015-03-08 16:15:37) Татьяна: Я думаю, в 3) неверно, так как там не указано, что окружности с одинаковым радиусом, а если это окружности с разными радиусами, то точка их пересечения будет не равноудалена от центров этих окружностей. А вообще, огромная Вам благодарность, спасибо за сайт.