
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ565 –Є–Ј 1087 |
 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=25 –Є CD=16 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=25 –Є CD=16 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Т–∞—А–Є–∞–љ—В вДЦ1
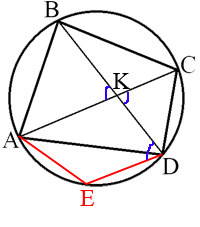 –Я—А–Њ–≤–µ–і–µ–Љ —Е–Њ—А–і—Г DE –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ AC.
–Я—А–Њ–≤–µ–і–µ–Љ —Е–Њ—А–і—Г DE –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ AC.
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ ACDE -
—В—А–∞–њ–µ—Ж–Є—П, –≤–њ–Є—Б–∞–љ–љ–∞—П –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Р —В–∞–Ї –Ї–∞–Ї —В–Њ–ї—М–Ї–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Г—О —В—А–∞–њ–µ—Ж–Є—О –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —В–Њ AE=CD=16.
∠AKB=∠CKD=60¬∞ (—В–∞–Ї –Ї–∞–Ї —Н—В–Њ
–≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–µ —Г–≥–ї—Л).
–Ґ–∞–Ї –Ї–∞–Ї AC –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ ED (–Љ—Л —Б–∞–Љ–Є —В–∞–Ї –њ—А–Њ–≤–µ–ї–Є), —В–Њ KD –Љ—Л –Љ–Њ–ґ–µ–Љ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М –Ї–∞–Ї —Б–µ–Ї—Г—Й—Г—О. –Ґ–Њ–≥–і–∞ ∠CKD=∠EDK=60¬∞ (—В–∞–Ї –Ї–∞–Ї —Н—В–Њ
–љ–∞–Ї—А–µ—Б—В –ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABDE.
–Ф–∞–љ–љ—Л–є —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї —В–Њ–ґ–µ –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Б—Г–Љ–Љ–∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л—Е —Г–≥–ї–Њ–≤ —А–∞–≤–љ–∞ 180¬∞ (–њ–Њ
—В–µ–Њ—А–µ–Љ–µ).
∠EAB+∠BDE=180¬∞
∠EAB=180¬∞-∠BDE
∠EAB=180¬∞-60¬∞=120¬∞
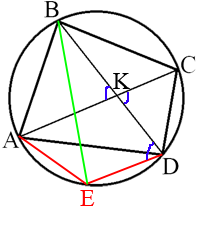 –Я—А–Њ–≤–µ–і–µ–Љ BE –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABE.
–Я—А–Њ–≤–µ–і–µ–Љ BE –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABE.
–Я–Њ —В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ –љ–∞–є–і–µ–Љ BE:
BE2=AB2+AE2-2AB*AE*cos∠EAB
BE2=252+162-2*25*16*cos120°
cos120¬∞=-1/2=-0,5 (–њ–Њ —В–∞–±–ї–Є—Ж–µ).
BE2=625+256-800*(-0,5)
BE2=1281
BE=√
–≠—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —В–Њ–ґ–µ –≤–њ–Є—Б–∞–љ –≤ —В—Г –ґ–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –Ј–∞–њ–Є—И–µ–Љ –і–ї—П –љ–µ–≥–Њ
—В–µ–Њ—А–µ–Љ—Г —Б–Є–љ—Г—Б–Њ–≤:
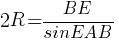
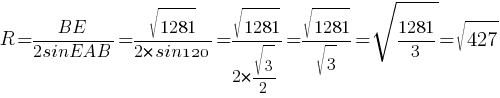
–Ю—В–≤–µ—В: √
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Э–∞–є–і–Є—В–µ –Њ—Б—В—А—Л–µ —Г–≥–ї—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –µ—Б–ї–Є –µ–≥–Њ –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞ —А–∞–≤–љ–∞ 20, –∞ –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 50√
–Э–∞–є–і–Є—В–µ –Њ—Б—В—А—Л–µ —Г–≥–ї—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –µ—Б–ї–Є –µ–≥–Њ –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞ —А–∞–≤–љ–∞ 20, –∞ –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 50√
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –Т —В—Г–њ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ –≤—Б–µ —Г–≥–ї—Л —В—Г–њ—Л–µ.
2) –Т –ї—О–±–Њ–Љ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –і–Є–∞–≥–Њ–љ–∞–ї–Є —В–Њ—З–Ї–Њ–є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–µ–ї—П—В—Б—П –њ–Њ–њ–Њ–ї–∞–Љ.
3) –Ґ–Њ—З–Ї–∞, –ї–µ–ґ–∞—Й–∞—П –љ–∞ —Б–µ—А–µ–і–Є–љ–љ–Њ–Љ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ –Ї –Њ—В—А–µ–Ј–Ї—Г, —А–∞–≤–љ–Њ—Г–і–∞–ї–µ–љ–∞ –Њ—В –Ї–Њ–љ—Ж–Њ–≤ —Н—В–Њ–≥–Њ –Њ—В—А–µ–Ј–Ї–∞.
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AB=CD, ∠BDA=62¬∞ –Є ∠BDC=42¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AB=CD, ∠BDA=62¬∞ –Є ∠BDC=42¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Э–∞–є–і–Є—В–µ BN, –µ—Б–ї–Є MN=12, AC=42, NC=25.
–Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Э–∞–є–і–Є—В–µ BN, –µ—Б–ї–Є MN=12, AC=42, NC=25.
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 800√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 800√

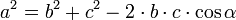
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2017-05-28 22:15:57) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: Alissa, —П –љ–µ –њ–Њ–љ—П–ї, –њ–Њ—З–µ–Љ—Г AC=25+16?
(2017-05-20 17:00:51) –Ы–∞–љ–∞: –Р –њ–Њ—З–µ–Љ—Г –Р–° —А–∞–≤–љ–Њ —Б—Г–Љ–Љ–µ —Б—В–Њ—А–Њ–љ?
(2017-05-20 11:08:36) Alissa: –•–Њ—З—Г –њ—А–µ–і–ї–Њ–ґ–Є—В—М –µ—Й—С –Њ–і–Є–љ –≤–∞—А–Є–∞–љ—В —А–µ—И–µ–љ–Є—П —Н—В–Њ–є –Ј–∞–і–∞—З–Є –±–µ–Ј –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ–Њ–≥–Њ –њ–Њ—Б—В—А–Њ–µ–љ–Є—П: –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Р–°D,–Р–°=25+16=41,–°D=16,—Г–≥–Њ–ї –°=60–≥—А.–Я–Њ —В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ –љ–∞–є–і—С–Љ —Б—В–Њ—А–Њ–љ—Г –РD=√1281. –Я–Њ—В–Њ–Љ –љ–∞–є–і—С–Љ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–°D –њ–Њ —Д–Њ—А–Љ—Г–ї–µ S=1/2*AC*DC*sinC, S=1/2*41*16*sin60=164√3. –Ю—Б—В–∞–ї–Њ—Б—М –љ–∞–є—В–Є R –њ–Њ —Д–Њ—А–Љ—Г–ї–µ R=(abc)/4S. R=(41*16*√1281)/4*164√3=√427. –Ю–Ґ–Т–Х–Ґ:√427
(2017-04-17 01:57:35) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Я–Њ –њ–Њ–≤–Њ–і—Г —В–µ–Њ—А–µ–Љ—Л —Б–Є–љ—Г—Б–Њ–≤ - –љ–µ —Б–Њ–≥–ї–∞—Б–µ–љ, –≤–µ–Ј–і–µ –≥–Њ–≤–Њ—А–Є—В—Б—П –Њ —А–∞–і–Є—Г—Б–µ –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –∞ –њ–Њ –њ–Њ–≤–Њ–і—Г —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Д–Њ—А–Љ—Г–ї—Л - —Б–Њ–≥–ї–∞—Б–µ–љ. –Я–Њ—Н—В–Њ–Љ—Г –њ—А–Є–≤–Њ–ґ—Г –µ—Й–µ –Њ–і–Є–љ –≤–∞—А–Є–∞–љ—В —А–µ—И–µ–љ–Є—П. –°–њ–∞—Б–Є–±–Њ –Ј–∞ —В–Њ, —З—В–Њ —Г–Ї–∞–Ј–∞–ї–Є –љ–∞ —Н—В–Њ—В —Д–∞–Ї—В.
(2017-04-12 10:53:23) : –Э–µ —Г–і–Є–≤–Є–ї–Њ, —З—В–Њ –і–ї—П —А–µ—И–µ–љ–Є—П –Ј–∞–і–∞—З–Є –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П —В–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б–Њ–≤, —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —А–∞–і–Є—Г—Б–∞ –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —Е–Њ—В—П —Н—В–Њ–≥–Њ –љ–µ—В –≤ —Г—З–µ–±–љ–Є–Ї–µ (–і–µ—В–Є –Љ–Њ–≥–ї–Є –і–Њ —Н—В–Њ–≥–Њ –і–Њ–є—В–Є —Б–∞–Љ–Є), –љ–Њ –≤ —А–µ—И–µ–љ–Є–Є –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–∞—П —Д–Њ—А–Љ—Г–ї–∞ —Б–Є–љ—Г—Б–∞ —А–∞–Ј–љ–Њ—Б—В–Є, –Њ–љ–∞ –Є–Ј—Г—З–∞–µ—В—Б—П —В–Њ–ї—М–Ї–Њ –≤ 10-–Љ –Ї–ї–∞—Б—Б–µ.
(2017-03-10 22:22:11) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ш–Љ–∞–љ, –Ь—Л –љ–µ –њ–Њ–Љ–Њ–≥–∞–µ–Љ —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –Х—Б–ї–Є –љ–∞–є–і–µ—В–µ –њ–Њ—Е–Њ–ґ—Г—О –Ј–∞–і–∞—З—Г –љ–∞ —Б–∞–є—В–µ fipi.ru, –Њ—В–њ—А–∞–≤—В–µ –Ј–∞—П–≤–Ї—Г –љ–∞ –і–Њ–±–∞–≤–ї–µ–љ–Є–µ –Ј–∞–і–∞—З–Є, –Є –Љ—Л –µ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–±–∞–≤–Є–Љ.
(2017-03-10 20:41:49) –Ш–Љ–∞–љ: –Ч–∞–і–∞—З–∞ 2. –С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ –Р –Є –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–Т–° –њ–µ—А–µ—Б–µ—З–µ–љ—Л –≤ —В–Њ—З–Ї–µ –Ь. –Э–∞–є–і–Є—В–µ –Р–Ь–Т, –µ—Б–ї–Є –Р = 58¬∞, –Т = 96¬∞. –Ч–∞–і–∞—З–∞ 3. –Э–∞–є–і–Є—В–µ —Г–≥–ї—Л —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –µ—Б–ї–Є: –∞) —Г–≥–Њ–ї –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –≤ –і–≤–∞ —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Г–≥–ї–∞, –њ—А–Њ—В–Є–≤–Њ–ї–µ–ґ–∞—Й–µ–≥–Њ –Њ—Б–љ–Њ–≤–∞–љ–Є—О; –±) —Г–≥–Њ–ї –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –≤ —В—А–Є —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ –≤–љ–µ—И–љ–µ–≥–Њ —Г–≥–ї–∞, —Б–Љ–µ–ґ–љ–Њ–≥–Њ —Б –љ–Є–Љ. –Ч–∞–і–∞—З–∞ 4. –Ь–µ–і–Є–∞–љ–∞ –Р–Ь —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–Т–° —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ —Б—В–Њ—А–Њ–љ—Л –Т–°. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Р–Т–° –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є. –Ч–∞–і–∞—З–∞ 5. –Ю–і–Є–љ –Є–Ј –≤–љ–µ—И–љ–Є—Е —Г–≥–ї–Њ–≤ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–µ–љ 115¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–ї—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
(2016-10-17 02:37:33) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –У–µ–Њ—А–≥–Є–є, –љ–Є—З–µ–≥–Њ —Б—В—А–∞—И–љ–Њ–≥–Њ, –ї–Є—И–љ–Є–є —А–∞–Ј –њ–µ—А–µ–њ—А–Њ–≤–µ—А–Є—В—М - –љ–µ –ї–Є—И–љ–µ–µ (–њ–∞—А–і–Њ–љ –Ј–∞ —В–∞–≤—В–Њ–ї–Њ–≥–Є—О). –Ш —Б–њ–∞—Б–Є–±–Њ –Ј–∞ –љ–∞–є–і–µ–љ–љ—Г—О –Њ–њ–µ—З–∞—В–Ї—Г.
(2016-10-17 01:55:06) –У–µ–Њ—А–≥–Є–є : –£–њ—Б... –Ю—В–≤–µ—В-—В–Њ –њ—А–∞–≤–Є–ї—М–љ—Л–є, –і–∞, —Н—В–Њ –≤—Б—С —П) –Ю—В–≤–µ—В "–Ї–Њ—А–µ–љ—М –Є–Ј 133" –Є–Ј –і—А—Г–≥–Њ–є –Ј–∞–і–∞—З–Є —В–∞–Ї–Њ–≥–Њ –ґ–µ —В–Є–њ–∞ –Є –њ–Њ—Е–Њ–ґ–Є–Љ, –љ–Њ —А–∞–Ј–љ—Л–Љ —Г—Б–ї–Њ–≤–Є–µ–Љ. –Ш–Ј–≤–Є–љ–Є—В–µ –Ј–∞ —В–∞–Ї–Њ–є —Г–ґ –њ–µ—А–µ–њ–Њ–ї–Њ—Е, –≤ —Ж–µ–ї–Њ–Љ —Б–њ–∞—Б–Є–±–Њ.)
(2016-10-17 00:05:27) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –У–µ–Њ—А–≥–Є–є, –њ—А–Њ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ —Г–≥–ї–Њ–≤ –Т—Л –њ—А–∞–≤—Л, –Є—Б–њ—А–∞–≤–ї–µ–љ–Њ. –Т –Њ—Б—В–∞–ї—М–љ–Њ–Љ –≤ —А–µ—И–µ–љ–Є–Є –Њ—И–Є–±–Њ–Ї –љ–µ –љ–∞–є–і–µ–љ–Њ. –Я–Њ –њ–Њ–≤–Њ–і—Г –Њ—В–≤–µ—В–∞: –≤ –і—А—Г–≥–Є—Е –Є—Б—В–Њ—З–љ–Є–Ї–∞—Е –і–∞–љ–љ–∞—П –Ј–∞–і–∞—З–∞ —А–µ—И–µ–љ–∞ –і—А—Г–≥–Є–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ, –љ–Њ –Њ—В–≤–µ—В –њ–Њ–ї—Г—З–Є–ї—Б—П —В–∞–Ї–Њ–є –ґ–µ –Ї–∞–Ї –Ј–і–µ—Б—М. –Э–∞–њ–Є—И–Є—В–µ, –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞, –Є–Ј –Ї–∞–Ї–Њ–≥–Њ –Є—Б—В–Њ—З–љ–Є–Ї–∞ –≤–Ј—П—В –Њ—В–≤–µ—В "–Ї–Њ—А–µ–љ—М –Є–Ј 133"?
(2016-10-16 23:43:40) –У–µ–Њ—А–≥–Є–є : (60-b) (–Њ–њ–µ—З–∞—В–∞–ї—Б—П) –Є –≤ –Њ—В–≤–µ—В–µ , –Ї—Б—В–∞—В–Є, –љ–∞–њ–Є—Б–∞–љ –Ї–Њ—А–µ–љ—М –Є–Ј 133. :/
(2016-10-16 23:38:20) –У–µ–Њ—А–≥–Є–є : AB/sin(/BCA)=2R => AB=2Rsin(/BCA). –Я–Њ—В–Њ–Љ –љ–∞–њ–Є—Б–∞–љ–Њ: /BCA=b /CBD=a –Є –і–∞–ї–µ–µ: AB=2Rsin(a). –†–∞–Ј–≤–µ –љ–µ –і–Њ–ї–ґ–љ–Њ –±—Л—В—М —В–∞–Ї: AB=2Rsin(b) –Є CD=2Rsin(b-60)?