
 На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
Прямая и окружность могут располагаться относительно друг друга в трех вариантах:
1) Не пересекаться, то есть не иметь ни одной общей точки.
2) Касаться, то есть иметь только одну общую точку, тогда прямая называется
касательной к окружности.
3) Пересекаться, то есть иметь две общие точки.
В условии задачи сказано, что окружность проходит через точку С и касается прямой ВС. Значит прямая ВС кроме точки касания других общих точек с окружностью иметь не может, следовательно, окружность касается с прямой ВС в точке С (как показано на рисунке).
Рассмотрим треугольники ABC и CDB.
∠B - общий
∠DAC является
вписанным в окружность и опирается на дугу CD. Т.е. равен половине ее градусной меры.
∠BCD обхватывает дугу CD как
касательная и
хорда и тоже равен половине градусной меры дуги CD (по
четвертому свойству углов).
Следовательно, углы DAC и BCD равны.
Тогда, по
первому признаку подобия треугольников, эти треугольники
подобны.
Следовательно:
AC/CD=BC/BD=AB/BC
AC/CD=BC/BD
12/8=18/BD =>BD=8*18/12=2*18/3=2*6=12
BC/BD=AB/BC
18/12=AB/18 => AB=18*18/12=9*18/6=9*3=27
AD=AB-BD=27-12=15
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
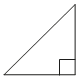 В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
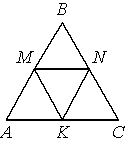 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
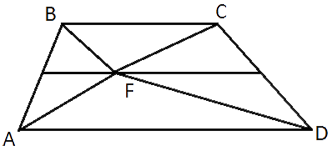 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.


Комментарии: