
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
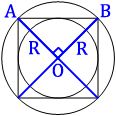 Проведем диаметры
описанной окружности, как показано на первом рисунке.
Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(38√
AB2=2*382*2
AB2=382*22=(38*2)2=762
AB=76
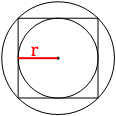 Проведем радиус
вписанной окружности, как на втором рисунке.
Проведем радиус
вписанной окружности, как на втором рисунке.
Очевидно, что:
r=AB/2=76/2=38
Ответ: 38
Поделитесь решением
Присоединяйтесь к нам...
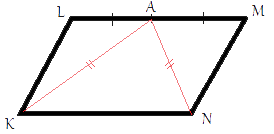 В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
 Площадь прямоугольного треугольника равна 18√
Площадь прямоугольного треугольника равна 18√
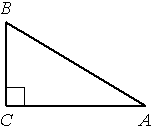 В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
 В трапеции
ABCD AB=CD, /BDA=67° и /BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции
ABCD AB=CD, /BDA=67° и /BDC=28°. Найдите угол ABD. Ответ дайте в градусах.

Комментарии: