Радиус вписанной в квадрат окружности равен 14√
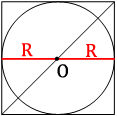Проведем радиусы окружности, как показано на рисунке.
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, т.е.:
a=2R=2*14√
По свойству квадрата, все углы прямые.
Следовательно, треугольник, образованный двумя сторонами и диагональю (обозначим ее как b) - прямоугольный.
Тогда можем применить теорему Пифагора:
b2=a2+a2
b2=2a2
b2=2(28√
b2=2*282*2
b2=282*22=(28*2)2=562
b=56
Ответ: 56
Поделитесь решением
Присоединяйтесь к нам...
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
Площадь прямоугольного треугольника равна 50√
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.
Найдите площадь треугольника, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-02-21 09:52:16) Администратор: Майкл, Вы правы, в решение вкралась ошибка. Спасибо большое, что заметили. Все исправлено!
(2019-02-21 00:54:00) Майкл: У вас получается , что лишь половина диагонали равно 28 , так как вы брали маленький треугольник , а просили Диагональ квадрата .Если а=14 корней из 2 ( то есть радиус , то тогда у вас диагональ меньше , чем сторона квадрата , а это невозможно.28 корней из двух больше 28