Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
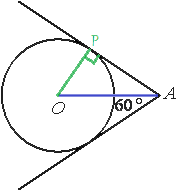Проведем отрезок АО, данный отрезок равен 8 (по условию задачи).
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР. Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР.
АО является биссектрисой угла, образованного касательными (свойство касательных прямых).
Соответственно угол РАО равен половине данного угла, т.е. 30°.
sin∠PAO=sin∠30°=1/2 (табличное значение).
sin∠PAO=ОР/АО (по определению синуса).
Получается:
ОР/АО=1/2
OP=AO/2=8/2=4 - это и есть радиус окружности.
Ответ: R=4.
Поделитесь решением
Присоединяйтесь к нам...
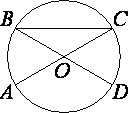В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
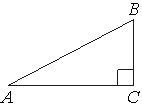В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: