Катеты прямоугольного треугольника равны 3√
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=212+(3√
AB2=441+9*51=441+459=900
AB=30
Меньший угол лежит напротив меньшей стороны, поэтому сравним числа 21 и 3√
212 и (3√
441 и 459, очевидно, что 441<459.
Следовательно 21<3√
Синус меньшего угла будет равен
отношению меньшей стороны к гипотенузе, т.е. 21/30=0,7
Ответ: 0,7
Поделитесь решением
Присоединяйтесь к нам...
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 55°. Найдите величину угла OAB.
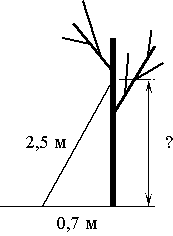Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока
до места крепления троса на земле равно 8 м. Найдите длину троса. Ответ дайте в метрах.
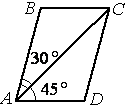Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
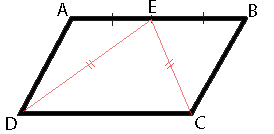В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: