В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
По условию задачи треугольник ABC -
равнобедренный.
BM является не только
медианой, но и
высотой (по
третьему свойству равнобедренного треугольника).
Следовательно:
1) AM=MC=AC/2=56/2=28
2) Треугольник ABM
прямоугольный.
Тогда, по
теореме Пифагора:
AB2=BM2+AM2
532=BM2+282
2809=BM2+784
BM2=2025
BM=45
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
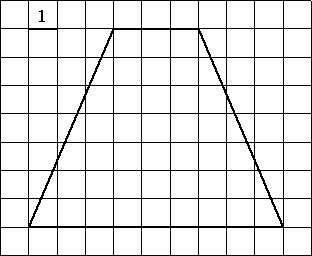Найдите площадь трапеции, изображённой на рисунке.
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
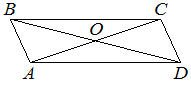Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
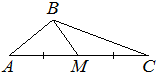В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.
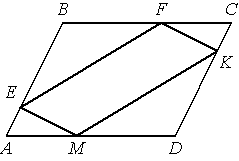В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: