
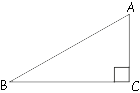
 Площадь прямоугольного треугольника равна 882√
Площадь прямоугольного треугольника равна 882√
 Площадь
прямоугольного треугольника равна половине произведения катетов:
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=882√
Пусть 60-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg60°=BC/AC=√
BC=AC√
S=AC*BC/2=AC*(AC√
AC2√
AC2/2=882
AC2=1764
AC=42
Ответ: 42
Поделитесь решением
Присоединяйтесь к нам...
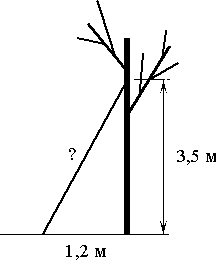 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
 Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
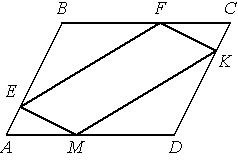 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
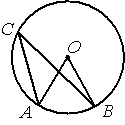 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).

Комментарии:
(2017-10-04 18:09:01) Администратор: Нигер228, квадратный корень из 1764 и есть 42.
(2017-10-03 22:00:15) Нигер228: Как мы из 1764 получили 42?
(2017-02-24 20:00:00) Администратор: Маша, через тангенс легче решать, потому, что и тангенс и площадь треугольника выражаются через катеты треугольника. Если решать через косинус или синус, то придется вводить еще одну неизвестную - гипотенузу, а это сильно усложнит решение.
(2017-02-24 18:30:27) маша: почему надо искать тангенс а не косинус или синус?