Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
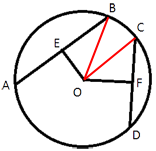Проведем отрезки OB и OC, как показано на рисунке.
Расстоянием от точки до прямой является длила перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои
хорды пополам (по
свойству хорды)
Получается, что треугольники OEB и OCF -
прямоугольные, EB=AB/2 и CF=CD/2.
По
теореме Пифагора:
OB2=OE2+EB2
OB2=82+(12/2)2
OB2=64+36=100
OB=10
OB=OC=10 (т.к. OB и OC - радиусы окружности)
По
теореме Пифагора:
OC2=CF2+FO2
OC2=(CD/2)2+FO2
102=(16/2)2+FO2
100=64+FO2
FO2=36
FO=6
Ответ: расстояние от центра окружности до хорды CD равно 6
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=18, DK=9, BC=16. Найдите AD.
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
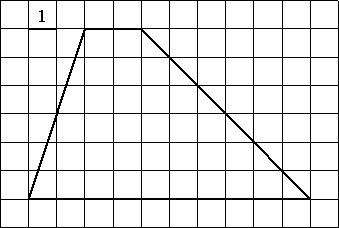Найдите площадь трапеции, изображённой на рисунке.
На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: