Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
Площадь
ромба равна S=ah, где a - сторона ромба, h - высота ромба.
AD=AH+HD=4+1=5.
AD=AB=BC=CD (по
определению ромба).
Рассмотрим треугольник ABH.
ABH -
прямоугольный (т.к. BH -
высота), тогда по
теореме Пифагора: AB2=BH2+AH2
52=BH2+42
25=BH2+16
BH2=9
BH=3
Sромба=AD*BH=5*3=15
Ответ: Sромба=15
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.
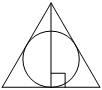Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
Косинус острого угла А треугольника равен 
. Найдите sinA.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-29 21:26:43) Администратор: Сабин, главное, что Вы сами все поняли, без подсказки.
(2014-05-29 21:14:17) Сабит: извините,это я не прав,я забыль,что ромб имеет все свойства квадрата,а у квадрата все стороны равны.
(2014-05-29 21:11:24) Сабит: Вы в формулу Пифагора подставили место AB в квадрате 5 в квадрате,а там сказано,что AD=5,а не AB.