
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
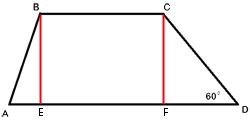 Проведем
высоты BE и CF как показано на рисунке.
Проведем
высоты BE и CF как показано на рисунке.
Рассмотрим треугольник CDF. Он
прямоугольный, т.к. CF-высота.
По
теореме о сумме углов треугольника /FCD=180°-90°-60°=30°.
По
определению синуса sin/FCD=DF/CD=sin30°=1/2
Т.е. DF=CD/2, CD, в свою очередь, по условию задачи равно AD/2, получам, что DF=AD/4.
BC=AD/2 (по условию задачи)
EF=BC=AD/2 (т.к. BCFE - прямоугольник)
Вычислим AE, AE=AD-DF-EF=AD-AD/4-AD/2=AD/4, т.е. мы получили, что AE=FD
Рассмотрим треугольники ABC и DCF:
BE=CF (т.к. BCFE - прямоугольник)
AE=FD (только что получили)
/AEF=90°=/DFC, тогда по
первому признаку равенства, треугольники ABC и DCF равны.
Следовательно, AB=CD, т.е. наша
трапеция равнобедренная.
AB=CD=4 (по условию задачи), AD=2*CD=2*BC=8 (тоже по условию), BC=CD=4
FD=AD/4=2
По
теореме Пифагора CD2=CF2+FD2
42=CF2+22
CF2=12, CF=√
CF=2√
SABCD=((BC+AD)/2)*CF=((4+8)/2)*2√
SABCD=12√
Ответ: SABCD=12√
Поделитесь решением
Присоединяйтесь к нам...
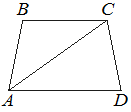 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
 В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
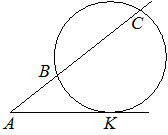 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
 Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.

Комментарии:
(2016-12-25 18:37:31) Администратор: Настя, 95, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-25 14:00:17) 95: Высота и отрезки на которые она делит сторону одного треугольника соответственно равны высоте и отрезкам на которые она делит сторону другого треугольника докажите что такие треугольники равны
(2016-12-25 14:00:15) 95: Высота и отрезки на которые она делит сторону одного треугольника соответственно равны высоте и отрезкам на которые она делит сторону другого треугольника докажите что такие треугольники равны
(2016-12-25 13:30:08) : Стороны треугольника пропорциональны числам 9:11:15 А разность наибольшее наименьшее сторон равна 18 см найдите периметр треугольника
(2016-12-25 13:28:28) Настя: Стороны треугольника пропали пропорциональны числам 09:11 11:15 а разность наибольшего и наименьшего сторон равна 18 см найдите периметр треугольника
(2016-12-18 17:29:20) Администратор: Настя, это первый признак равенства треугольников, доказательство данной теоремы Вы найдете в любом учебнике по геометрии.
(2016-12-18 15:03:47) Настя: BE=CF,AE=DF ,угол 1= углу 2 Доказать: треугольник ABD= треугольнику DCA