Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Рассмотрим каждое утверждение.
1) "Через две различные точки на плоскости проходит единственная прямая", это утверждение верно (
свойство прямой).
2) "Центром вписанной в треугольник окружности является точка пересечения его биссектрис", это утверждение верно (
свойство вписанной окружности).
3) "Если гипотенуза и острый угол одного
прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны". Прилежащий к известному острому углу катет равен проиведению косинуса этого угла на гипотенузу (из
определения косинуса). Следовательно этот катет тоже будет равен у обоих треугольников. Тогда по
первому признаку равенства, получается, что эти треугольники равны. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
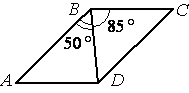Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Радиус окружности, описанной около квадрата, равен 16√
Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: