
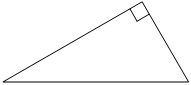
 Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
Обозначим неизвестный острый угол как α.
В
прямоугольном треугольнике один из углов прямой, т.е. равен 90°.
Тогда, по теореме о сумме углов треугольника:
180°=57°+90°+∠α
180°=147°+∠α
∠α=180°-147°
∠α=33°
Ответ: 33
Поделитесь решением
Присоединяйтесь к нам...
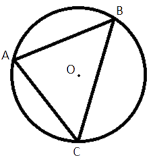 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
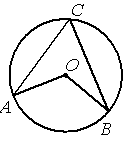 Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.

Комментарии: