Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
Рассмотрим треугольники ABC и MBN.
/B - общий.
/BAC=/BMN (т.к. это
соответственные углы)
/BCA=/BNM (т.к. это тоже
соответственные углы)
Следовательно, эти треугольники
подобны по
первому признаку подобия.
Тогда по
определению подобных треугольников:
AC/MN=BC/BN
AC/MN=BC/(BC-NC)
51/17=BC/(BC-32)
3=BC/(BC-32)
3(BC-32)=BC
3BC-96=BC
2BC=96
BC=48
BN=BC-NC=48-32=16
Ответ: BN=16
Поделитесь решением
Присоединяйтесь к нам...
Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
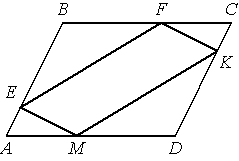В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: