Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Рассмотрим каждое утверждение.
1) "Против большей стороны треугольника лежит меньший угол", это утверждение неверно, т.к. противоречит
теореме о соотношении углов и сторон.
2) "Любой
квадрат можно вписать в
окружность", это утверждение верно, т.к. четырехугольник можно вписать в окружность, если сумма противоположных углов этого четырехугольника равна 180°.
3) "Площадь
трапеции равна произведению
средней линии на высоту", это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника BKP к площади треугольника AMK.
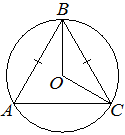Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
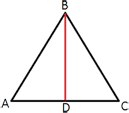Сторона равностороннего треугольника равна 10√
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: