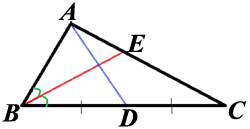В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Вариант №1
Рассмотрим треугольник ABD.
BO перпендикулярен AD (по условию задачи), т.е. ∠BOD=∠BOA=90°.
∠ABO=∠DBO (т.к. BE -
биссектриса).
Получается, что треугольники ABO и DBO равны (по
второму признаку равенства треугольников).
Следовательно, AB=BD.
Т.е. треугольник ABD -
равнобедренный.
BO -
биссектриса этого треугольника, следовательно и
медиана, и
высота (по третьему
свойству равнобедренного треугольника).
Следовательно, AO=OD=AD/2=44/2=22.
Проведем отрезок ED и рассмотрим треугольник BEC.
ED -
медиана этого треугольника, так как делит сторону BC пополам.
Площади треугольников EDC и EDB равны (по второму
свойству медианы).
SEDC=SEDB=(BE*OD)/2=(44*22)/2=22*22=484
SABE=(BE*AO)/2=(44*22)/2=484
Т.е. SABE=SEDC=SEDB=484
Тогда, SABС=3*484=1452
AD -
медиана треугольника ABC (по условию), следовательно делит треугольник на два равных по площади треугольника ABD и ACD (по
второму свойству медианы).
SABD=(AD*BO)/2=SABC/2
(44*BO)/2=1452/2
BO=1452/44=33
Рассмотрим треугольник ABO, он
прямоугольный, тогда применим
теорему Пифагора:
AB2=BO2+AO2
AB2=332+222
AB2=1089+484=1573
AB=√
BC=2AB=2*11√
Рассмотрим треугольник AOE.
OE=BE-BO=44-33=11
Так как этот треугольник тоже
прямоугольный, то можно применить
теорему Пифагора:
AE2=AO2+OE2
AE2=222+112=484+121=605
AE=√
Так как BE -
биссектриса, то используя ее
первое свойство запишем:
BC/AB=CE/AE
22√
2=CE/(11√
CE=22√
AC=AE+CE=11√
Ответ: AB=11√
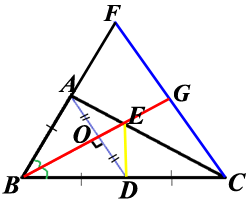Проведём через точку C прямую, параллельную AD. Продлим BA и BE до пересечения с этой прямой в точках F и G соответственно.Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: