На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
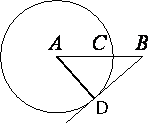Проведем отрезок AD, где D - точка касания
окружности и
касательной.
AD перпендикулярен к
касательной (по
свойству касательной), т.е. угол между AD и
касательной DB равен 90°.
Следовательно, треугольник ABD -
прямоугольный.
AD=AC=6 (т.к. это радиусы окружности и, соответственно, равны друг другу).
По
теореме Пифагора: AB2=AD2+BD2
(AC+BC)2=AD2+BD2
(6+4)2=62+BD2
100=36+BD2
BD2=64
BD=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB=9.
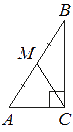В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
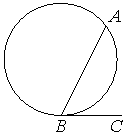На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: