Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
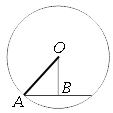Обозначим ключевые точки, как показано на рисунке. Проведем отрезок АО.
Рассмотрим треугольник AOB.
Данный треугольник
прямоугольный, так как расстояние ОВ является
высотой (кротчайшее расстояние).
AB равна половине длины
хорды (по
третьему свойству хорды).
Тогда, по
теореме Пифагора:
AO2=OB2+AB2
AO2=722+(130/2)2
AO2=5184+4225=9409
AO=97 - это радиус окружности, следовательно, диаметр:
D=2*AO=2*97=194
Ответ: 194
Поделитесь решением
Присоединяйтесь к нам...
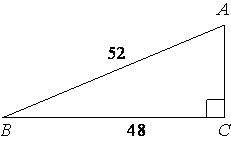Найдите площадь треугольника, изображённого на рисунке.
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
Косинус острого угла A треугольника ABC равен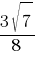 
. Найдите sinA.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
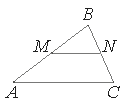Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-05-16 18:52:08) Милана: Дана окружность с центром О, через который проходят две хорды. Найди < D AB, если