
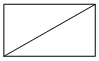
 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Площадь
прямоугольника равна произведению его сторон.
По
определению, все углы прямоугольника прямые, следовательно, диагональ и две стороны образуют
прямоугольный треугольник.
Следовательно, мы можем применить
теорему Пифагора, обозначим длину неизвестной стороны как "х":
962+x2=1002
x2=1002-962
Можно вычислить "в лоб", а можно немного облегчить себе задачу, применив формулу
разность квадратов:
x2=(100-96)(100+96)
x2=4*196
x=√
S=96*28=2688
Ответ: 2688
Поделитесь решением
Присоединяйтесь к нам...
 Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
30° и 105° соответственно.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
30° и 105° соответственно.
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
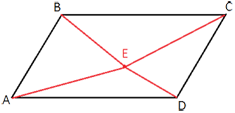 Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
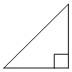 В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
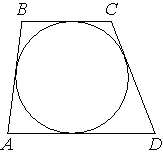 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.

Комментарии: