Катеты прямоугольного треугольника равны 3√
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=212+(3√
AB2=441+9*51=441+459=900
AB=30
Меньший угол лежит напротив меньшей стороны, поэтому сравним числа 21 и 3√
212 и (3√
441 и 459, очевидно, что 441<459.
Следовательно 21<3√
Синус меньшего угла будет равен
отношению меньшей стороны к гипотенузе, т.е. 21/30=0,7
Ответ: 0,7
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь треугольника, изображённого на рисунке.
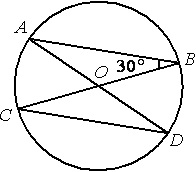В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
В трапеции ABCD AB=CD, ∠BDA=10° и ∠BDC=109°. Найдите угол ABD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: