
 Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
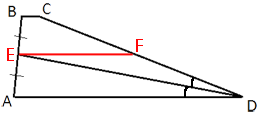 Проведем отрезок, параллельный основаниям, как показано на рисунке.
Проведем отрезок, параллельный основаниям, как показано на рисунке.
EF -
средняя линия трапеции, так как соединяет середины боковых сторон трапеции (по
теореме Фалеса).
∠ADE=∠DEF (так как это
накрест-лежащие углы при параллельных прямых EF и AD и секущей ED).
Получается, что ∠DEF=∠EDF (так как DE -
биссектриса).
Значит треугольник EFD -
равнобедренный (по
свойству равнобедренного треугольника).
Следовательно, EF=FD (по
определению).
EF=FD=CD/2=15/2=7,5
EF=(BC+AD)/2=7,5
(3+AD)/2=7,5
3+AD=15
AD=12
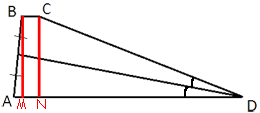 Проведем
высоты как показано на рисунке.
Проведем
высоты как показано на рисунке.
MN=BC=3 (т.к. BCNM -
прямоугольник).
BM=CN=h
Обозначим AM как x, для удобства.
AD=AM+MN+ND
12=x+3+ND
ND=9-x
Для треугольника ABM запишем
теорему Пифагора:
AB2=h2+x2
122=h2+x2
h2=144-x2
Для треугольника CDN запишем
теорему Пифагора:
CD2=h2+ND2
152=h2+(9-x)2
225=h2+(9-x)2
Подставляем вместо h2 значение из первого уравнения:
225=144-x2+(9-x)2
225-144=-x2+92-2*9*x+x2
81=92-2*9*x
81=81-18x
18x=0
x=0, получается, что BM совпадает со стороной AB, т.е. AB является высотой трапеции.
Тогда площадь трапеции равна:
S=AB(AD+BC)/2=12(12+3)/2=6*15=90
Ответ: 90
Поделитесь решением
Присоединяйтесь к нам...
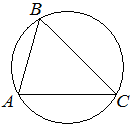 В треугольнике ABC угол C равен 45°, AB=6√
В треугольнике ABC угол C равен 45°, AB=6√
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл) | Прочее оборудование и монтаж | Средн. расход газа/ средн. потребл. мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 24 000 руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 000 руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт*ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости устройства газового и электрического отопления?
 Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
 Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
 Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Комментарии: