
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ500 –Є–Ј 1087 |
 –Ю–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–і–Є—Г—Б–Њ–≤ 44 –Є 77 –Ї–∞—Б–∞—О—В—Б—П –≤–љ–µ—И–љ–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ. –Ґ–Њ—З–Ї–Є A –Є B –ї–µ–ґ–∞—В –љ–∞ –њ–µ—А–≤–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —В–Њ—З–Ї–Є C –Є D вАФ –љ–∞ –≤—В–Њ—А–Њ–є. –Я—А–Є —Н—В–Њ–Љ AC –Є BD вАФ –Њ–±—Й–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –њ—А—П–Љ—Л–Љ–Є AB –Є CD.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–і–Є—Г—Б–Њ–≤ 44 –Є 77 –Ї–∞—Б–∞—О—В—Б—П –≤–љ–µ—И–љ–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ. –Ґ–Њ—З–Ї–Є A –Є B –ї–µ–ґ–∞—В –љ–∞ –њ–µ—А–≤–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —В–Њ—З–Ї–Є C –Є D вАФ –љ–∞ –≤—В–Њ—А–Њ–є. –Я—А–Є —Н—В–Њ–Љ AC –Є BD вАФ –Њ–±—Й–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –њ—А—П–Љ—Л–Љ–Є AB –Є CD.
–†–µ—И–µ–љ–Є–µ –њ—А–µ–і–ї–Њ–ґ–Є–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Р–ї–µ–Ї—Б–∞–љ–і—А –Ъ—А—Г—В—М
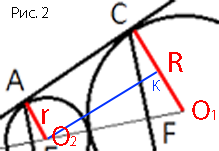
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ
—В—А–∞–њ–µ—Ж–Є—О ACO1O2
–Ф–∞–љ–љ–∞—П —В—А–∞–њ–µ—Ж–Є—П
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–∞—П, —В.–Ї. —А–∞–і–Є—Г—Б—Л –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л
–Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є AC (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є).
–Я—А–Њ–≤–µ–і–µ–Љ O2K –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ AC, O2K=AC, —В.–Ї. ACKO2 -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
 –Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
(O1O2)2=(O2K)2+(KO1)2
(R+r)2=(O2K)2+(R-r)2
(77+44)2=(O2K)2+(77-44)2
14641=(O2K)2+1089
(O2K)2=13552
O2K=√
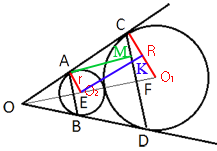 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AM, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л–є CD. AM —А–∞–≤–љ—П–µ—В—Б—П –Є—Б–Ї–Њ–Љ–Њ–Љ—Г EF, —В–∞–Ї –Ї–∞–Ї AMFE –Њ–±—А–∞–Ј—Г–µ—В –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AM, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л–є CD. AM —А–∞–≤–љ—П–µ—В—Б—П –Є—Б–Ї–Њ–Љ–Њ–Љ—Г EF, —В–∞–Ї –Ї–∞–Ї AMFE –Њ–±—А–∞–Ј—Г–µ—В –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ACM –Є O2KO1.
∠O2KO1=∠AMC=90¬∞
∠KO2O1=CAM (—В–∞–Ї –Ї–∞–Ї —Б—В–Њ—А–Њ–љ—Л —Г–ї–Њ–≤ –њ–Њ–њ–∞—А–љ–Њ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л (–њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г).
–Ґ–Њ–≥–і–∞:
AM/O2K=AC/O2O1
–Э–∞–њ–Њ–Љ–љ–Є–Љ: AC –Љ—Л –љ–∞—И–ї–Є —А–∞–љ–µ–µ, O2K=AC, O2O1=R+r.
AM/AC=AC/(R+r)
AM=AC*AC/(R+r)
AM=(44√
AM=442*7/121
AM=13552/121=112
–Ю—В–≤–µ—В: 112
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Б —В—Г–њ—Л–Љ —Г–≥–ї–Њ–Љ ACB –њ—А–Њ–≤–µ–і–µ–љ—Л –≤—Л—Б–Њ—В—Л AA1 –Є BB1. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є A1CB1 –Є ACB –њ–Њ–і–Њ–±–љ—Л.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Б —В—Г–њ—Л–Љ —Г–≥–ї–Њ–Љ ACB –њ—А–Њ–≤–µ–і–µ–љ—Л –≤—Л—Б–Њ—В—Л AA1 –Є BB1. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є A1CB1 –Є ACB –њ–Њ–і–Њ–±–љ—Л.
–Ф–≤–µ —В—А—Г–±—Л, –і–Є–∞–Љ–µ—В—А—Л –Ї–Њ—В–Њ—А—Л—Е —А–∞–≤–љ—Л 7 —Б–Љ –Є 24 —Б–Љ, —В—А–µ–±—Г–µ—В—Б—П –Ј–∞–Љ–µ–љ–Є—В—М –Њ–і–љ–Њ–є, –њ–ї–Њ—Й–∞–і—М –њ–Њ–њ–µ—А–µ—З–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–љ–∞ —Б—Г–Љ–Љ–µ –њ–ї–Њ—Й–∞–і–µ–є –њ–Њ–њ–µ—А–µ—З–љ—Л—Е —Б–µ—З–µ–љ–Є–є –і–≤—Г—Е –і–∞–љ–љ—Л—Е. –Ъ–∞–Ї–Є–Љ –і–Њ–ї–ґ–µ–љ –±—Л—В—М –і–Є–∞–Љ–µ—В—А –љ–Њ–≤–Њ–є —В—А—Г–±—Л? –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ —Б–∞–љ—В–Є–Љ–µ—В—А–∞—Е.
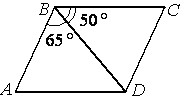 –Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
65¬∞ –Є 50¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
65¬∞ –Є 50¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
 –Э–∞ —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –Њ—В–Љ–µ—З–µ–љ–∞ —В–Њ—З–Ї–∞ D —В–∞–Ї, —З—В–Њ AD=3, DC=7. –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–∞ 20. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BCD.
–Э–∞ —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –Њ—В–Љ–µ—З–µ–љ–∞ —В–Њ—З–Ї–∞ D —В–∞–Ї, —З—В–Њ AD=3, DC=7. –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–∞ 20. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BCD.
–°–Ї–Њ–ї—М–Ї–Њ –і–Њ—Б–Њ–Ї –і–ї–Є–љ–Њ–є 4 –Љ, —И–Є—А–Є–љ–Њ–є 20 —Б–Љ –Є —В–Њ–ї—Й–Є–љ–Њ–є 30 –Љ–Љ –≤—Л–є–і–µ—В –Є–Ј –±—А—Г—Б–∞ –і–ї–Є–љ–Њ–є 80 –і–Љ, –Є–Љ–µ—О—Й–µ–≥–Њ –≤ —Б–µ—З–µ–љ–Є–Є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї —А–∞–Ј–Љ–µ—А–Њ–Љ 30 —Б–Љ –љ–∞ 40 —Б–Љ?

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2017-04-24 01:47:07) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р–ї–µ–Ї—Б–∞–љ–і—А, —Б–њ–∞—Б–Є–±–Њ –±–Њ–ї—М—И–Њ–µ. –Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ, –Т–∞—И–µ —А–µ—И–µ–љ–Є–µ –љ–∞–Љ–љ–Њ–≥–Њ —Г–і–Њ–±–љ–µ–є –Є –Ї–Њ—А–Њ—З–µ. –Я—Г–±–ї–Є–Ї—Г—О –µ–≥–Њ –њ–Њ–і –Т–∞—И–Є–Љ –Є–Љ–µ–љ–µ–Љ.
(2017-04-20 07:07:40) –Р–ї–µ–Ї—Б–∞–љ–і—А: –≠—В–Њ –µ—Й–µ –љ–µ —Б–∞–Љ–Њ–µ —Г–і–Њ–±–љ–Њ–µ —А–µ—И–µ–љ–Є–µ. –Т—Л—И–ї—О –њ–Њ—З—В–Њ–є.
(2017-04-19 18:52:37) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р–ї–µ–Ї—Б–∞–љ–і—А, —П –њ—А–Є—Б–ї—Г—И–∞–ї—Б—П –Ї –Т–∞—И–µ–Љ—Г —Б–Њ–≤–µ—В—Г –Є —Б–Њ–≥–ї–∞—Б–µ–љ —Б –Т–∞–Љ–Є. –ѓ –њ–Њ–і–Њ–±—А–∞–ї –љ–∞–Є–±–Њ–ї–µ–µ —Г–і–Њ–±–љ—Л–µ –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є –Є –њ–µ—А–µ–і–µ–ї–∞–ї —А–µ—И–µ–љ–Є–µ —З–µ—А–µ–Ј –њ–Њ–і–Њ–±–Є–µ. –Ю—В–≤–µ—В —Б–Њ—И–µ–ї—Б—П —Б –Т–∞—И–Є–Љ. –°–њ–∞—Б–Є–±–Њ –±–Њ–ї—М—И–Њ–µ –Ј–∞ –њ–Њ–і—Б–Ї–∞–Ј–Ї—Г.
(2017-04-18 22:26:29) –Р–ї–µ–Ї—Б–∞–љ–і—А: –Ъ —В–Њ–Љ—Г –ґ–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ —В—А–Є–≥–Њ–љ–Њ–Љ–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –≤ –і–њ–љ–љ–Њ–є –Ј–∞–і–∞—З–µ –Є–Ј–ї–Є—И–љ–µ–µ, –Љ–Њ–ґ–љ–Њ –њ—А–Њ—Б—В–Њ —З–µ—А–µ–Ј –њ–Њ–і–Њ–±–Є–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –С—Г–і–µ—В –њ—А–Њ—Й–µ.
(2017-04-18 15:26:52) –Р–ї–µ–Ї—Б–∞–љ–і—А: –†–µ—И–µ–љ–Є–µ —Б–Њ–і–µ—А–ґ–Є—В –Њ—И–Є–±–Ї—Г. –Я—А–∞–≤–Є–ї—М–љ—Л–є –Њ—В–≤–µ—В 112.
(2016-09-27 13:01:37) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ш—А–Є–љ–∞, —Б–њ–∞—Б–Є–±–Њ –±–Њ–ї—М—И–Њ–µ, –Є—Б–њ—А–∞–≤–ї–µ–љ–Њ.
(2016-09-27 08:28:01) –Є—А–Є–љ–∞: –Њ–њ–µ—З–∞—В–Ї–∞. –†–∞—Б—Б–Љ. —В—А–µ—Г–≥.–Ю–Р–Ю2 –Є –Ю–°–Ю1 (—Б–Љ. —А–Є—Б.1)
(2015-12-26 00:54:05) –У–∞–ї–Є–љ–∞: –°–њ–∞—Б–Є–±–Њ!!!