
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ492 –ł–∑ 1087 |
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, sinA=7/17, AC=4√
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, sinA=7/17, AC=4√
–ü–ĺ
–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é: sinA=BC/AB => BC=AB*sinA=AB*7/17
–ü–ĺ
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ü–ł—Ą–į–≥–ĺ—Ä–į:
AB2=BC2+AC2
AB2=(AB*7/17)2+(4√
AB2-(AB*7/17)2=16*15
AB2(1-(7/17)2)=240
AB2(289/289-49/289)=240
AB2*240/289=240
AB2=289
AB=17
–ě—ā–≤–Ķ—ā: AB=17
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
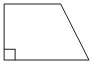 –ě–ī–ł–Ĺ –ł–∑ —É–≥–Ľ–ĺ–≤ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł —Ä–į–≤–Ķ–Ĺ 121¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –ľ–Ķ–Ĺ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ —ć—ā–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–ě–ī–ł–Ĺ –ł–∑ —É–≥–Ľ–ĺ–≤ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł —Ä–į–≤–Ķ–Ĺ 121¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –ľ–Ķ–Ĺ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ —ć—ā–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –Ě–į–Ļ–ī–ł—ā–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–Ě–į–Ļ–ī–ł—ā–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
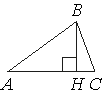 –í –ĺ—Ā—ā—Ä–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–į –≤—č—Ā–ĺ—ā–į BH, ∠BAC=37¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABH. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–í –ĺ—Ā—ā—Ä–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–į –≤—č—Ā–ĺ—ā–į BH, ∠BAC=37¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABH. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–ö–į–ļ–ł–Ķ –ł–∑ –ī–į–Ĺ–Ĺ—č—Ö —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ –≤–Ķ—Ä–Ĺ—č? –ó–į–Ņ–ł—ą–ł—ā–Ķ –ł—Ö –Ĺ–ĺ–ľ–Ķ—Ä–į.
1) –ß–Ķ—Ä–Ķ–∑ –ī–≤–Ķ —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–į—Ź –Ņ—Ä—Ź–ľ–į—Ź.
2) –¶–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ—á–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ķ–≥–ĺ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā.
3) –ē—Ā–Ľ–ł –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į –ł –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ –ĺ–ī–Ĺ–ĺ–≥–ĺ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ä–į–≤–Ĺ—č –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–Ķ –ł —É–≥–Ľ—É –ī—Ä—É–≥–ĺ–≥–ĺ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —ā–ĺ —ā–į–ļ–ł–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł —Ä–į–≤–Ĺ—č.
 –í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –Ī–ĺ–ļ–ĺ–≤–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–į AB –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—é BC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ–ł C –ł D –ł –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AB –≤ —ā–ĺ—á–ļ–Ķ E. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł E –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ CD, –Ķ—Ā–Ľ–ł AD=14, BC=7.
–í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –Ī–ĺ–ļ–ĺ–≤–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–į AB –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—é BC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ–ł C –ł D –ł –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AB –≤ —ā–ĺ—á–ļ–Ķ E. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł E –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ CD, –Ķ—Ā–Ľ–ł AD=14, BC=7.

–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2015-05-24 20:34:29) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –ö–į—ā—Ź, –ľ—č AB2 –≤—č–Ĺ–Ķ—Ā–Ľ–ł –∑–į —Ā–ļ–ĺ–Ī–ļ–ł.
(2015-05-24 20:20:41) –ö–į—ā—Ź: –Ņ–ĺ—á–Ķ–ľ—É –Ĺ–į —ą–Ķ—Ā—ā–ĺ–Ļ —Ā—ā—Ä–ĺ–ļ–Ķ –≤ —Ä–Ķ—ą–Ķ–Ĺ–ł–ł –Ĺ–į–Ņ–ł—Ā–į–Ĺ–ĺ 1 –≤–ľ–Ķ—Ā—ā–ĺ –ź–í? –ü–ĺ—Ź—Ā–Ĺ–ł—ā–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į —ą–Ķ—Ā—ā–ĺ–Ļ —Ā—ā—Ä–ĺ—á–ļ–Ķ)