Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Площадь любого треугольника равна половине произведения
высоты и стороны, к которой
высота проведена.
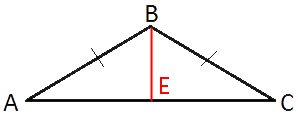
Проведем
высоту как показано на рисунке.
По
свойству равнобедренного треугольника BE - и
высота, и
медиана. Следовательно, AE=EC=AC/2.
Треугольник ABE -
прямоугольный (т.к. BE -
высота).
По
теореме Пифагора найдем высоту BE:
AB2=AE2+BE2
AB2=(AC/2)2+BE2
342=(60/2)2+BE2
1156=900+BE2
BE2=256
BE=16
SABC=(BE*AC)/2=(16*60)/2=16*30=480
Ответ: SABC=480
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
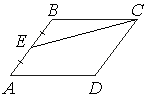Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 5 м. Найдите длину троса.
Площадь прямоугольного треугольника равна 32√
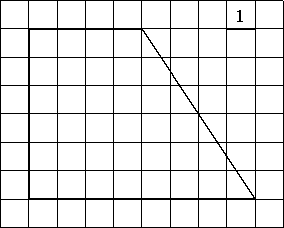Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-28 22:37:16) Администратор: Павел, правильно заданный вопрос - это половина правильного ответа )))
(2014-05-28 21:36:02) Павел: Только написал и сразу понял
(2014-05-28 21:35:07) Павел: Откуда в 4 строчке 900?