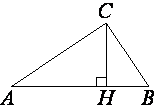
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
82=(2√
64=4*15+AH2
AH2=64-60
AH2=4
AH=2
sin∠ACH=AH/AC (по
определению)
sin∠ACH=2/8=1/4=0,25
Как было выведено выше:
sin∠ABC=sin∠ACH=0,25
Ответ: sin∠ABC=0,25
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 37°, угол ABC равен 25°. Найдите угол ACB. Ответ дайте в градусах.
Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
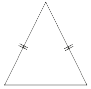Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-05-11 09:37:59) Администратор: Олеся, к сожалению, у меня нет такой информации.
(2016-05-11 09:36:57) Олеся: Ответьте пожалуйста, на экзамене эта задача под каким номером. Из второй части?
(2016-05-11 09:32:39) Олеся: Ответьте пожалуйста, на экзамене эта задача под каким номером. Из второй части?