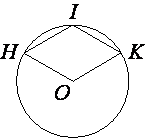Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OHI. Ответ дайте в градусах.
HO=KO (т.к. это радиусы окружности)
HO=KO=HI=IK (по
определению ромба)
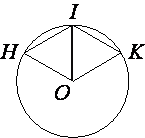Проведем отрезок OI.
OI тоже радиус окружности, следовательно HO=KO=HI=IK=OI
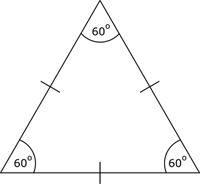
Следовательно, треугольники HIO и KIO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно, /OHI=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Углы при одном из оснований трапеции равны 48° и 42°, а отрезки, соединяющие середины противоположных сторон трапеции равны 6 и 3. Найдите основания трапеции.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
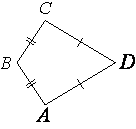В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: