Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Рассмотрим треугольник ALD.
AL вдвое меньше AB (по условию задачи).
AD тоже вдвое меньше AB (по условию задачи), следовательно:
AL=AD
Т.е. данный треугольник
равнобедренный.
По
свойству равнобедренного треугольника ∠ADL=∠ALD
∠ALD=∠LDC (т.к. это
накрест-лежащие углы).
Получается, что ∠ADL=∠LDC.
Следовательно DL -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
Сколько досок длиной 4 м, шириной 20 см и толщиной 30 мм выйдет из бруса длиной 80 дм, имеющего в сечении прямоугольник размером 30 см на 40 см?
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
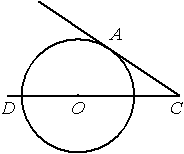Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
110°.
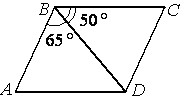Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол параллелограмма.
Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Треугольника со сторонами 1, 2, 4 не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: