В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
Так как AB=CD, значит трапеция ABCD -
равнобедренная.
Тогда по
свойству равнобедренной трапеции ∠ABC=∠BCD=123° и ∠CDA=∠DAB.
Вспомнив, что сумма углов выпуклого n-угольника вычисляется по формуле (n-2)180°, получим, что сумма углов трапеции равна (4-2)180°=360°.
Тогда ∠ABC+∠BCD+∠CDA+∠DAB=360°
123°+123°+∠CDA+∠DAB=360°
∠CDA+∠DAB=360°-123°-123°=114°
∠CDA=∠DAB=114°/2=57°
Рассмотрим треугольник ACD.
Так как AC=AD, то данный треугольник -
равнобедренный.
Следовательно, по
свойству равнобедренного треугольника
∠CDA=∠DCA=57°
∠BCA=∠BCD-∠DCA=123°-57°=66°
∠BCA=∠CAD=66° (т.к. они
накрест-лежащие для параллельных прямых AD и BC).
Ответ: 66
Поделитесь решением
Присоединяйтесь к нам...
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
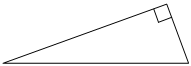В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
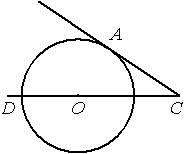Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-06-04 08:57:41) учитель математики: А меж тем эта задача была в ГИА-2014 в варианте 704
(2014-06-03 09:55:32) Администратор: Согласен, я даже не могу нарисовать рисунок, чтобы он полностью удовлетворял условию...
(2014-06-03 06:42:58) учитель математики: Задача некорректна. Угол BAD равен 57 градусов, а угол CAD должен быть меньше, т.к. составляет часть от него.
(2014-05-20 21:44:56) Администратор: 360°-123°-123°=114° (добавлено в решение)
(2014-05-20 17:14:40) : А как появилось 114