В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
Так как BM -
медиана, значит AM=MC=AC/2=97/2=48,5
Рассмотрим треугольник MBC.
Т.к. BC=BM (по условию задачи), значит этот треугольник
равнобедренный, BH -
высота этого треугольника. По
третьему свойству равнобедренного треугольника MH=HC=MC/2=48,5/2=24,25
Искомая AH=AC-HC=97-24,25=72,75
Ответ: AH=72,75
Поделитесь решением
Присоединяйтесь к нам...
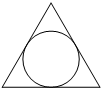Радиус окружности, вписанной в равносторонний треугольник, равен 2√
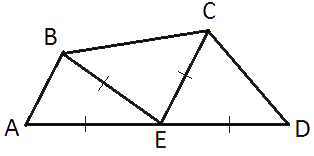Середина M стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°.
Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
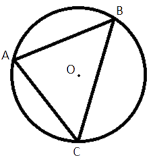Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: