Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
По
свойству
равнобедренного треугольника:
высота, проведенная к основанию так же является и
медианой.
Следовательно, AD=DC=AC/2=60/2=30
Чтобы вычислить эту высоту треугольника воспользуемся
теоремой Пифагора:
AB2=BD2+AD2
342=BD2+302
1156=BD2+900
BD2=256
BD=16
Площадь треугольника: S=ah/2
S=60*16/2=480
Ответ: S=480
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
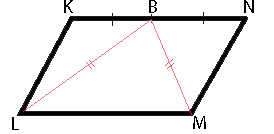В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: