Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите этот диаметр, если диаметр описанной окружности треугольника ABC равен 8.
Рассмотрим рисунок. Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с
биссектрисой BM (по
свойству описанной окружности).
Рассмотрим треугольники BMP и CPM:
MP - общая сторона
BP=PC (по условию задачи)
/BPM=/CPM, т.к. /BPM - прямой, а /CPM - ему
смежный.
Следовательно треугольники BMP и CPM равны (по
первому признаку). Отсюда следует, что BM=MC=MA.
Рассмотрим треугольник BMC. Т.к. MB=MC, то этот треугольник
равнобедренный, следовательно /MCP=/PBM (по
свойству равнобедренных треугольников).
В треугольнике ABM аналогичная ситуация, /BAM=/ABM.
Т.е. получается, что /BAM+/MCP=/ABC. Из
теоремы о сумме углов треугольника следует, 180°=/BAM+/MCP+/ABC
180°=/ABC+/ABC
180°=2*/ABC
90°=/ABC
Из чего следует, что треугольник ABC -
прямоугольный. По
свойству описанной окружности следует, что точка М - центр описанной окружности => AC - диаметр описанной окружности, AM - радиус описанной окружности = AC/2=4. А так как BM=AM (мы это выяснили выше), то BM тоже равен 4.
Ответ: BM=4.
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
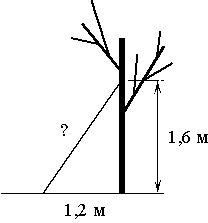Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: