Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Периметр
параллелограмма:
P=AB+BC+CD+AD
AB=CD и BC=AD (по
свойству параллелограмма)
P=AB+BC+AB+BC=2(AB+BC)
∠DAK=∠AKB (т.к. это
накрест-лежащие углы).
Следовательно ∠AKB=∠KAB (т.к. AK -
биссектриса)
Получается, что треугольник ABK -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BK=7
P=2(AB+BC)=2(AB+BK+KC)=2(7+7+12)=52
Ответ: 52
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 2√
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
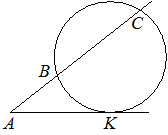Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: